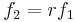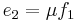Bond graph

A bond graph is a graphical representation of a physical dynamic system. It is similar to the better known block diagram and signal-flow graph, with the major difference that the arcs in bond graphs represent bi-directional exchange of physical energy, while those in block diagrams and signal-flow graphs represent uni-directional flow of information. Also, bond graphs are multi domain and domain neutral. This means a bond graph can incorporate multiple domains seamlessly.

The Bond Graph is composed of the "bonds" which link together "single port", "double port" and "multi port" elements (see below for details). Each bond represents the instantaneous flow of energy (dE/dt) or power. The flow in each bond is denoted a pair of variables called 'power variables' whose product is the instantaneous power of the bond. For example, the bond of an electrical system would represent the flow of electrical energy and the power variables would be voltage and current, whose product is power. Each domain's power variables are broken into two types: "effort" and "flow". Effort multiplied by flow produces power, thus the term power variables. Every domain has a pair of power variables with a corresponding effort and flow variable. Examples of effort include force, torque, voltage, or pressure; while flow examples include velocity, current, and volumetric flow. The table below contains the most common energy domains and the corresponding "effort" and "flow".

A bond has two other features described briefly here, and discussed in more detail below. One is the "half-arrow" sign convention. This defines the assumed direction of positive energy flow. As with electrical circuit diagrams and free-body diagrams, the choice of positive direction is arbitrary, with the caveat that the analyst must be consistent throughout with the chosen definition. The other feature is the "causal stroke". This is a vertical bar placed on only one end of the bond. It is not arbitrary. As described below, there are rules for assigning the proper causality to a given port, and rules for the precedence among ports. Any port (single, double or multi) attached to the bond shall specify either "effort" or "flow" by its causal stroke, but not both. The port attached to the end of the bond with the "causal stroke" specifies the "flow" of the bond. And the bond imposes "effort" upon that port. Equivalently, the port on the end without the "causal stroke" imposes "effort" to the bond, while the bond imposes "flow" to that port. This is made more clear with the illustrative examples below.

Energy Domain effort e symbol e unit (metric) e unit (imperial) flow f symbol f unit (metric) f unit (imperial)
Mechanical, translation Force F N lb Linear velocity v m/s ft/s, mph
Mechanical, rotation Torque τ N·m ft·lb Angular velocity ω rad/s rad/s
Electrical Electromotive force V or u V V Current I or i A A
Magnetic [1] Magnetomotive force Flux rate
Hydraulic Pressure P Pa psi Volumetric flow rate Q m³/s ft^3/s
Thermal temperature T °C or K °F entropy flow rate S W/°C ft·lb/s·°F

If the dynamics of the physical system to be modeled operate on widely varying time scales, fast continuous-time behaviors can be modeled as instantaneous phenomena by using a hybrid bond graph.

Contents

History

The Bond Graph was invented by Henry Paynter.[2]. The term "Bond Graph" comes from the fact that many of these graphs look like the bonds in chemistry; an example of this structure is shown in the 'examples' section of this wiki.[3].

Basics

The fundamental idea of a bond graph is that power is transmitted between connected components by a combination of "effort" and "flow" (generalized effort & generalized flow). Refer to the table above for examples of effort and flow in different domains. If an engine is connected to a wheel through a shaft, the power is being transmitted in the rotational mechanical domain, meaning the effort and the flow are torque (τ) and angular velocity (ω) respectively. A word bond graph is a first step towards a bond graph, in which words define the components. As a word bond graph, this system would look like:

           τ
engine ---------- wheel
           ω

A half-arrow is used to provide a sign convention, so if the engine is doing work when τ and ω are positive, then the diagram would be drawn:

           τ
engine ---------- wheel
           ω    /

A full arrow is used to indicate a measurement, and are referred to as signal bonds, because the amount of power flowing through the bond is insignificant. However, it may be useful to certain physical components. For example, the power required to activate a relay is orders of magnitude smaller than the power through the relay itself; making it relevant only to convey whether the switch is on, not the power consumed by it.

               \
wheel ---------- tachometer
          ω    /

Junctions

Power bonds may join at one of two kinds of junctions: a 0 junction and a 1 junction.

For an example of a 1 junction, consider a resistor in series:

v1 ---\/\/\/\---v2
i1       R      i2=i1

In this case, the flow (current) is constrained to be the same at all points, and when the implied current return path is included the efforts sum to zero. Power can be computed at points 1 and 2, and in general some power will be dissipated in the resistor. As a bond graph, this becomes

       R
       |\
  v1   |   v2
------ 1 ------
  i1 /     i2 /

From an electrical point of view, this diagram may seem counterintuitive in that flow is not preserved in the same way across the diagram. It may be helpful to consider the 1 junction as daisy chaining the bonds it connects to and power bond up to the R as a resistor with a lead returning back down, so the above is equivalent to

       R
    +\/\/\+
     \   /
      | |
  v1  | |  v2
------+ +------
  i1       i2

Regardless of the problem domain, bond graph modeling typically proceeds from the identification of key 1 and 0 junctions associated with identifiable efforts and flows in the system, then identifying the dissipative (R) and storage elements (L and C), power sources, and drawing bonds wherever power or information flow between the sources, junctions, and storage/dissipative components. Then sign conventions (arrow heads), and causality are assigned, and finally equations describing the behavior of the system can be derived using the graph as a kind of guide or map.

Causality

Bond graphs have a notion of causality, indicating which side of a bond determines the instantaneous effort and which determines the instantaneous flow. In formulating the dynamic equations that describe the system, causality defines, for each modeling element, which variable is dependent and which is independent. By propagating the causation graphically from one modeling element to the other, analysis of large-scale models becomes easier. Completing causal assignment in a bond graph model will allow the detection of modeling situation where an algebraic loop exists; that is the situation when a variable is defined recursively as a function of itself.

As an example of causality, consider a capacitor in series with a battery. It is not physically possible to charge a capacitor instantly, so anything connected in parallel with a capacitor will necessarily have the same voltage (effort variable) as the capacitor. Similarly, an inductor cannot change flux instantly and so any component in series with an inductor will necessarily have the same flow as the inductor. Because capacitors and inductors are passive devices, they cannot maintain their respective voltage and flow indefinitely—the components to which they are attached will affect their respective voltage and flow, but only indirectly by affecting their current and voltage respectively.

Note: Causality is a symmetric relationship. When one side "causes" effort, the other side "causes" flow.

Active components such as an ideal voltage or current source are also causal.

In bond graph notation, a causal stroke may be added to one end of the power bond to indicate that the opposite end is defining the effort. Consider a constant-torque motor driving a wheel. That would be drawn as follows:

  motor      τ    \|
     SE  ----------| wheel
             ω     |

Symmetrically, the side with the causal stroke (in this case the wheel) defines the flow for the bond.

Causality results in compatibility constraints. Clearly only one end of a power bond can define the effort and so only one end of a bond can have a causal stroke. In addition, the two passive components with time-dependent behavior, I and C, can only have one sort of causation: an I component determines flow; a C component defines effort. So from a junction, J, the only legal configurations for I and C are

         \|
 J -------| I
          |

and

   |      \
 J |------- C
   |

A resistor has no time-dependent behavior: you can apply a voltage and get a flow instantly, or apply a flow and get a voltage instantly, thus a resistor can be at either end of a causal bond:

         \|               |       \

          |               |

Sources of flow define flow, sources of effort define effort. Transformers are passive, neither dissipating nor storing energy, so causality passes through them:

        | ..      |          |       .. |
  ------| TF -----|    or    |------ TF |------
        |         |          |          |

A gyrator transforms flow to effort and effort to flow, so if flow is caused on one side, effort is caused on the other side and vice versa:

  |       ..      |                | .. |     
  |------ GY -----|    or    ------| GY |------
  |               |                |    |
Junctions

In a 0-junction, efforts are equal; in a 1-junction, flows are equal. Thus, with causal bonds, only one bond can cause the effort in a 0-junction and only one can cause the flow in a 1-junction. Thus, if the causality of one bond of a junction is known, the causality of the others is also known. That one bond is called the strong bond

                ___
                 |
                 |
                 |

         ------| 0 ------|
strong bond ^
                 |
                 |
                 |
                ---

                 |
                 |
                 |
                --- 
         |------ 1 |------
strong bond ^   ___
                 |
                 |
                 |

One can continue, assigning causality using the above rules. Any model which results in inconsistent causality is not physically valid. For example, consider an inductor in series with an ideal current source—a physically impossible configuration. The bond graph would look like

 SF ------ 1 ------ I

Assigning causality to the source bond we get:

 SF |----- 1 ------ I

Propagating the causality through the junction gives

 SF |----- 1 |----- I

But assigning causality to the inductor gives

 SF |----- 1 |----| I

which is invalid, because the causality on the right bond is redundant. This ability to automatically identify impossible configurations is a major advantage of bond graphs.

In contrast, one can inadvertently draw an electrical diagram or mechanical schematic that, while possible to construct, would not behave as modeled. For example, one can connect a capacitor directly to a battery, but the assumption that the battery is an ideal voltage source would be violated corresponding with the fact that the theoretical flux would be infinite. The bond graph would tell you that a resistor needs to be put in series with the capacitor to keep the model realistic.

Example

Consider a simple RC circuit[4]:

        R
 i1 --\/\/\-----+------ i2 →
 v1             |       v2
              C =  ↓ic
                |
     ground ----+------

As a bond graph, the same system looks like

               R          C
              ---
               |\         |\
               |          |
                         ---
       v1   |     |            v2  \
Se,in ------|  1  |-----  0  ------- out
       i1  /|     |    /       i2  /

Note that the output is assumed to draw no power from the circuit, so a full arrow is used instead of a half-arrow. For the purpose of modeling dynamics, this means the output full bond can be ignored and the diagram is simplified:

                R
               ---
                |\
             v3 | i3
                |
        v1   |     | v2
S_e,in ------|  1  |-----  C
        i1  /|     | i2 /

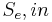S_e,in is a "source of effort" (voltage source) that forces the dynamics. Note that the causality for a source of effort imposes effort on the junction. To avoid formulating integral equations, the causality stroke for the capacitor must also impose effort on the junction. Since every 1 junction should have exactly one flow causal stroke, bond 3 must show flow imposed by the R element (causal stroke away from 1 junction).

To derive the differential equation, start on bond 2 (attached to a reactive element) and write the capacitive relation:

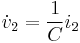
\dot{v}_2 = {1 \over C} i_2

Because bond 2 is attached to a 1 junction (shared flow) where bond 3 determines the flow, 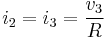i_2 = i_3 = {v_3 \over R}. In turn, following the effort causality on the 1 junction we can write 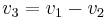v_3 = v_1 - v_2 so:

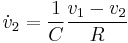
\dot{v}_2 = {1 \over C} { { v_1 - v_2 } \over R}

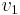Since v_1 is an input, and 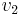v_2 is a state variable, the equation is completely expanded. For systems with multiple I and/or C elements, the process can be repeated once for each derivative of a state variable and a system of (typically linear) differential equations can be formed.

For example, suppose we put two of these in series:

        R             → i2     R              
 i1 --\/\/\-----+------------\/\/\-----+------ i3 →
 v1             |       v2             |       v3
              C = ↓ic               C = ↓ic
                |                      |
     ground ----+----------------------+---------

The corresponding bond graph looks like

           R          C          R         C
          ---                   ---
           |\         |\         |\        |\
         6 |        4 |        2 |       3 |
                     ---                  ---
     1   |   |  5          7   |   |  8        9  \
SE ------| 1 |------  0  ------| 1 |------ 0 ------ out
        /|   |     /          /|   |     /        /

where the ever-present effort/flow (voltage/current in this case) variables have been dropped and the bonds are simply numbered per typical bond graph convention (in this case the first four numbers were placed to avoid confusion with the signal numbering in the circuit diagram). Again, the output is assumed to draw no power so bonds 8 and 9 can effectively be removed in favor of a direct connection to bond 3:

           R          C          R
          ---                   ---
           |\         |\         |\
         6 |        4 |        2 |
                     ---              
     1   |   |  5          7   |   |  3
SE ------| 1 |------  0  ------| 1 |------ C
        /|   |     /          /|   |     /

As before, we can start with the derivative of a state variable (v4) and follow the bonds to form equations:

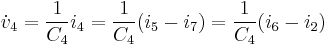
\dot{v}_4 = {1 \over C_4} i_4 = {1 \over C_4} (i_5 - i_7) = {1 \over C_4} (i_6 - i_2)

Continuing the expansion:

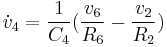
\dot{v}_4 = {1 \over C_4} ({v_6 \over R_6} - {v_2 \over R_2})

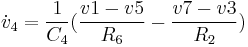
\dot{v}_4 = {1 \over C_4} ({{v 1 - v 5} \over R_6} - {{v 7 - v 3} \over R_2})

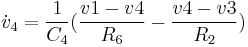
\dot{v}_4 = {1 \over C_4} ({{v 1 - v 4} \over R_6} - {{v 4 - v 3} \over R_2} )

Grouping by state variables and inputs:

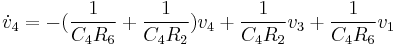
\dot{v}_4 = -({1 \over {C_4 R_6}} %2B {1 \over {C_4 R_2}}) v_4 %2B {1 \over {C_4 R_2}} v_3 %2B { 1 \over {C_4 R_6}} v_1

Similarly, \dot{v}_3 can be obtained:

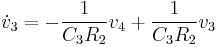
\dot{v}_3 = -{1 \over {C_3 R_2}} v_4 %2B {1 \over {C_3 R_2}} v_3

from which state equations can be formed:

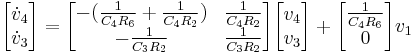\begin{bmatrix}\dot{v}_4 \\ \dot{v}_3\end{bmatrix} = \begin{bmatrix}-({1 \over {C_4 R_6}} %2B {1 \over {C_4 R_2}}) & {1 \over {C_4 R_2}} \\ -{1 \over {C_3 R_2}} & {1 \over {C_3 R_2}} \end{bmatrix} \begin{bmatrix}v_4\\v_3\end{bmatrix} %2B \begin{bmatrix}{ 1 \over {C_4 R_6} } \\ 0 \end{bmatrix} v_1.

Other components

Transformer

A transformer adds no power but transforms it, much as an ideal electrical transformer or a lever.

Denoted

         r
   e1   ..   e2
------- TF ------ 
   f1        f2

where the r denotes the modulus of the transformer. This means

f_2 = r f_1 \,

and

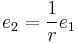e_2 = \frac{1}{r} e_1 \,.

Gyrator

A gyrator relates flow to effort. It also adds no power and is written

   e1   μ   e2
------- GY ------ 
   f1        f2

meaning that

e_2 = \mu f_1 \,

and

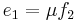e_1 = \mu f_2 \,.

See also

International Conferences on Bond Graph Modeling (ECMS & ICBGM)

A bibliography on Bond Graph modeling may be extracted from the following conferences :

References

  1. ^ Karnopp, D. C., Rosenberg, R. C. and Margolis, D. L., 1990: System dynamics: a unified approach, Wiley, ISBN 0-471-62171-4.
  2. ^ Paynter, Henry M., "Analysis and Design of Engineering Systems", The M.I.T. Press, ISBN 0262160048.
  3. ^ Karnopp, Dean C., "System Dynamics- Modeling and Simulation of Mechetronic Systems",John Wiley and Sons Inc., ISBN 0471709654.
  4. ^ www.mech.gla.ac.uk/Research/Control/Publications/Reports/csc99005.ps

Further reading

External links